Avertissement

Cet article pédagogique s’adresse à un public familier avec des notions de géométrie, notamment de trigonométrie (sinus, cosinus et tangente), et des notions de base de géographie, et en particulier les définitions de la latitude, des tropiques, et de l’écliptique. Si malgré mon rappel ci-dessous vous écarquillez toujours vos yeux en grand devant ces notions, je vous invite à consulter votre site de référence préféré sur ces termes, puis à revenir continuer la lecture de cet article, qui vous apparaîtra bien plus clair ainsi.

Notations utilisées

Le réel pi sera noté π dans la suite.
Les angles seront exprimés ou entendus en degrés, car on travaille en géographie, et non en radians comme c’est traditionnellement la cas en trigonométrie.

Rappels

Géométrie

• coordonnées polaires : c’est un système de coordonnées du plan à deux variables : le rayon r et l’angle θ, décrivant la position d’un point dans des problèmes à symétrie circulaire ou elliptique. Le point est à la distance r d’un centre de rotation, ou d’un foyer s’il s’agit d’une ellipse. L’angle θ prendra dans cet article des valeurs comprises entre 0 et 360°.
• génératrice de cône : c’est une droite qui, lors de sa rotation autour d’un axe (différent d’elle-même), va généré un cône. Pour vulgariser le concept, imaginez que vous saisissez une tige par un bout et que vous faites des moulinets avec votre poignet sans bouger votre bras. La tige est la génératrice d’un cône, car en tournant autour de l’axe de votre avant-bras elle dessine virtuellement un cône dans l’air.

Trigonométrie

• cosinus : dans un triangle rectangle, il s’agit du rapport côté adjacent / hypoténuse . Il varie dans l’intervalle [-1, 1]
• sinus : il s’agit du rapport côté opposé / côté adjacent . Opposé dans le sens "opposé à l’angle considéré". Il varie également dans l’intervalle [-1, 1], mais s’annule quand le sinus fleurit, et vice-versa.
• tangente : il s’agit du rapport sinus / cosinus . Il varie dans l’intervalle [-∞, +∞]
• arctangente : c’est la fonction réciproque de tangente, c’est l’angle pour lequel tangente vaut la valeur considérée.
  e.g. arctan(1) = 45°, car tan(45°) = 1.

Géographie

• latitude : c’est un angle, exprimé en degrés, qui définit votre position Nord-Sud. Il peut varier de -90° (pôle sud) à 90° (pôle nord), en passant ar la valeur nulle sous l’équateur.
• tropiques : ce sont les limites sur Terre que le zénith du soleil (endroit où le soleil est vu à la verticale d’un observateur) ne dépassera jamais. En d’autres termes le soleil à la verticale oscille entre les tropiques nord (Cancer) et sud (Capricorne). Au nord du Cancer le soleil ne passera jamais à la verticale, idem au sud du Capricorne.
  Les tropiques ont actuellement^R1 une latitude de 23°26’15" nord (Cancer) et 23°26’15" sud (Capricorne).
• écliptique : il s’agit de la trajectoire apparente de la Terre sur son orbite autour du soleil. La Terre est actuellement ^R1 inclinée sur son écliptique de ε=23°26’, de telle façon que le Soleil la voit sous un angle différent chaque jour (voir l’expérience cognitive ci-dessous).

Activité cognitive

Je voudrais vous faire toucher du doigt l’impact de l’existence de l’inclinaison de la terre sur les saisons. C’est l’inclinaison qui créé la succession des saisons, et leur retour chaque année (plus ou moins en beauté, mais ça c’est un autre problème).
Pour que vous viviez vous-même la conséquence pratique de cette inclinaison du globe sur l’écliptique, rendez-vous chez un marchand de globes terrestres, par exemple Nature et Découvertes, sans contrat particulier avec eux… Allez-y avec un ami.
Tenez vous de part et d’autre d’un globe posée sur l’étagère, et comparez quelle proportion des pôles vous pouvez chacun voir. Vous comprenez maintenant pourquoi en tournant autour du soleil, le soleil voit chaque jour un peu plus ou un peu moins des calottes polaires ?

Interprétation :
Comme on peut le voir sur le schéma ci-dessous, selon où vous vous positionnez par rapport au globe, et en le levant à autour de vos yeux, vous verrez peut-être la totalité de la calotte Antarctique, ou Arctique, ou exactement la moitié. Sur le schéma la lumière du soleil est représentée par les grosses flèches jaunes. Vos yeux qui regardent le globe c’est un peu comme le soleil qui regarderait la terre. Eh bien figurez-vous que le soleil lui aussi est soumis à ces vues selon le jour de l’année. On va le voir ci-après.

Bien, alors revenons à notre problème de départ : la brillance ressentie. Nous sommes tous d’accord que pour un même ciel dégagé, l’été, la lumière nous apparaît bien plus forte qu’en hiver. Celui provient tout simplement de l’angle d’incidence de la lumière par rapport à l’horizontale, disons le sol.
En effet, un rayon lumineux en provenance du soleil traversera d’autant plus de matière absorbante (les différentes couches d’air et de gaz en général composant l’atmosphère. Comme disait M. Rebufié, mon prof de biologie de Terminale C, "c’est le principe de la tranche de salami que l’on coupe en biais ou droite : sa largeur dépend de l’angle de coupe".

Nous voilà donc avec notre loi première : Pour un même ciel dégagé, la clarté ressentie est d'autant plus grande que le soleil est haut dans le soleil.
Inversement, elle est d'autant plus atténuée que le soleil est bas par rapport à l'horizon.

A partir de ce point, et pour toute la suite de l’article, je vais faire l’hypothèse que l’observateur (vous !) a au dessus de lui un ciel dégagé. Le ciel couvert est trop complexe à gérer car non quantifiable.

Quantifier le ressenti de clarté

Maintenant je vais tenter de définir une quantité capable de qualifier le ressenti de brillance. C’est nécessaire dans ma démonstration de travailler avec des quantités, de façon à me désolidariser de la subjectivité.
Il est toujours sensible de quantifier un ressenti, puisqu’il est par nature qualitatif. Mais je mets carte sur table, je choisis le point de culmination, c’est-à-dire la hauteur maximale du soleil pour le jour considéré. Par la suite j’appelerai la date de culmination le jour et l’heure exacte du point de culmination.
Pour simplifier mon analyse, je fais l’hypothèse que le ressenti qui marquera la mémoire de mon observateur pour ce jour est la clarté qui fut observée par lui autour de l’heure du Point de culmination, c’est à dire quand le soleil passe le plus haut dans le ciel ce jour-là.

Bon, j’ai perdu personne ? Si le paragraphe ci-dessus n’est pas clair, prenez tranquillement le temps de le relire, car maintenant vient le côté plus technique, mais je vais m’efforcer de rester seulement géométrique et simple le plus longtemps possible pour ne perdre personne en route. Si par la suite vous ne comprenez pas une démonstration, ce n’est pas grave, il vous suffira d’accepter le théorème (loi) qui suivra, puis de continuer la lecture.

Eh bien après tout ça, on distille directement notre loi seconde, toujours dans l’hypothèse du ciel dégagé, mais cette hypothèse a été prise avant je vous le rappelle. Pour un jour donné, le ressenti de clarté en un lieu est proportionnel¹ à la hauteur du point de culmination.

Ok, alors tout ça vous paraît peut-être un peu trivial jusque-là, mais comme toujours en science, il faut avancer à coup de loi démontrées, petit-à-petit, et faire les approximations qui s’imposent, et prendre des hypothèses de travail plausibles.

Donc vous voulez du hardcore ? On va essayer de le limiter, mais il y en aura, je vous le promets.

Je vais tenter de me passer d’équation le plus longtemps possible, en faisant appel le plus possible au bon sens. D’ailleurs, n’est-ce pas le rêve des profs de prépa que de vouloir que leurs étudiants reviennent au bon sens lorsqu’ils sont empêtrés dans leurs équations ?

Ces culminations nouvelles à vos yeux…

Je vous rappelle ce que l’on recherche : des culminations nouvelles à vos yeux. En plus haut ou en plus bas d’ailleurs. On va voir quand on est dans un cas ou un autre.

Loi n°3

Soit un observateur qui se trouve en P à la latitude λ_P,
soit le soleil, à cette époque de l’année, qui passe au zénith à la latitude λ_S,
alors le soleil culminera à midi² à une hauteur

h = 90°-(λP - λS)

Sa démonstration est donnée un peu plus bas.

On en déduit ses corollaires C3 et C3’ :
Si vous voyagez en vous rapprochant de l'équateur, alors le soleil pourra culminer en B, quelque part dans l'année, plus haut que vous n'ayez jamais connu à votre point de départ A. Si vous voyagez en vous rapprochant d'un pôle, alors le soleil ne pourra culminer en B, quelque part dans l'année, que plus bas que vous n'ayez jamais connu en A à toute époque de l'année.

Mais qu’est-ce que ça veut dire que ce truc-là ? Ca veut dire que si vous habitez en Norvège (A) par exemple, et que vous vous rendiez en Nouvelle-Calédonie (B), il faut vous attendre à ce que le soleil, en été, connaisse des hauteurs qui vont dépasser celles vous n’avez jamais connues en Norvège. En effet, vous vous êtes rapproché de l’équateur, car la latitude de la Nouvelle-Calédonie est bien inférieure à la latitude de la Norvège si l’on fait abstraction du signe + ou -, par convention Nord ou Sud respectivement.

Un autre exemple : si vous habitez à Brisbane, en Australie (A), et que vous vous rendez à Paris (B), en hiver à Paris le soleil culminera à des hauteurs plus basses que celles que vous n’ayez jamais connues à Brisbane quelle que soit l’époque de l’année, car Paris est plus proche d’un pôle que Brisbane ne l’est.

On peut comprendre ce que ça veut dire : en introduction je disais qu’à cause de l’inclinaison de la terre sur on écliptique, le soleil passe à la verticale, donc le plus haut possible, à des lieux géographiques qui se répartissent dans la ceinture inter-tropicale. Donc plus vous vous rapprochez d’un pôe et plus vous dites bye-bye à cette verticalité. Donc son passage culminant se fera de plus en plus bas à mesure que vous vous éloignez d’un pôle.

Vocabulaire

Souvenez-vous des latitudes basses (sous-entendu en valeur absolue) comme étant celles des lieux plus proches de tropiques, et à fortiori de l’équateur (0°, il n’y a pas plus bas !), et des latitudes hautes (sous-entendu en valeur absolue) comme étant celles des lieux plus proches des cercles polaires et à fortiori des pôles (90°, il n’y a pas plus haut, Nord au Sud, on parlera quand même de haute latitude).

Démonstration de la loi n°3

Attention, les latitudes λ sont comptées négativement dans l’hémisphère sud. Ici dans l’exemple, λ_S est négative, donc λ_P - λ_S est l’angle somme des angles absolus.

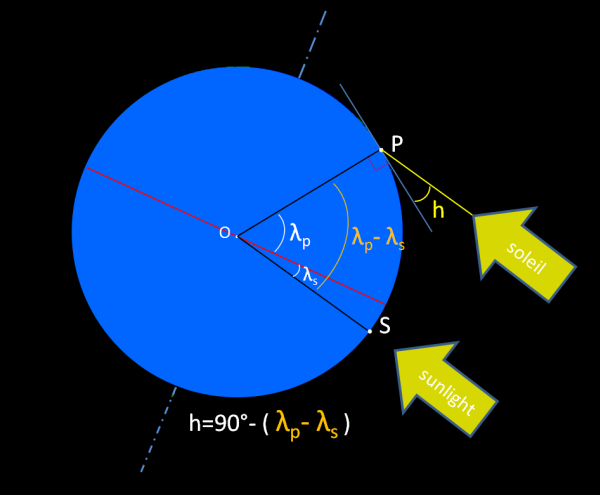
Graphiquement on comprend bien d’où provient le 90° moins… :
si λ_P = λ_S , c’est à dire l’observateur est exactement sous le soleil, qui passe au zénith à midi donc ; alors pour chaque degré dont il va marcher vers le nord par exemple, c’est un degré de moins pour le soleil par rapport au zénith de l’observateur, car le pauvre soleil lui, ne s’est pas déplacé d’un degré vers le nord… Ce qui provoque une culmination réduite à 89°. Pour un degré additionnel dont il va marcher vers le nord, le soleil ne culminera qu’à 88°, etc. En fait, pour Δ degrés plus au nord, le soleil ne passera à sa hauteur maximale qu’à 90-Δ degrés.
On en déduit sans peine que pour une différence de latitude Δ = λ_P - λ_S , compté positivement si P est au nord de S, c’est bien 90° - (λ_P - λ_S) qui sera la hauteur maximale du soleil à midi.

Et ça fonctionne pareil pour un déplacement vers le sud : si l’observateur marche d’un degré vers le sud, le soleil passera à un degré de plus de sa verticale, donc 90°+1° au dessus de l’horizon. Si l’observateur continue son déplacement vers le sud, il passera à 92°, soit 2° de plus que la verticale, etc. On a bien que 92°=90°-(-2°), -2° car l’observateur s’est cette fois-ci déplacé vers le sud.

En l’appliquant à un voyage vers l’équateur, pour nous placer dans le cadre du corollaire C3, on diminue λ_P, donc on fait augmenter la culmination du soleil (car λ_S est fixée à une date donnée, et s’applique globalement, indépendemment du point P considéré.
A l’inverse, lors d’un voyage vers un pôle, on augmente λ_P vers des valeurs plus hautes qu’en A, dans le cas de l’hémisphère nord, ou tellement négatives dans le cas de l’hémisphère sud que le soleil bascule bien au delà de la verticale à midi, et donc dans les deux cas la culmination du soleil se rapproche de l’horizon, horizon sud ou horizon nord, selon l’hémisphère.

On en déduit un corollaire : En tout lieu situé au 'nord du soleil'³, à midi le soleil passe au sud. et sa réciproque En tout lieu situé au 'sud du soleil'³, à midi le soleil passe au nord.

Toutefois, on notera que le soleil provoquera la même luminosité s’il est à +n degrés par rapport à la verticale ou -n degrés par rapport à la verticale. Donc, pour tenir compte du fait que la latitude est une grandeur algébrique, c’est à dire porteuse d’un signe + ou -, on va induire dans la Loi n°3 la fonction valeur absolue, qui fait désolidariser de l’appartenance à un hémisphère ou à un autre. Ainsi la loi n°3 s’écrit globalement :

h = 90°-( |λP| - λS)

où |x| représente la valeur absolue de x.

Corollaire : à Melbourne, en Australie, donc bien au sud du tropique du Capricorne, le soleil se lève à l'est, passe au nord à midi puis se couche à l'ouest. Mais à Cairns, toujours en Australie, un lieu situé à presque 17°S, soit -17°, donc entre l'équateur et le tropique du Capricorne, mais plutôt près du tropique, alors le soleil passe au nord à midi la plupart de l'année, mais connaît des dates de passage au sud de Cairns, lorsque la latitude du soleil³ λ_S est inférieure (= plus au sud) à la latitude de la ville.

Détermination des dates de lumière inconnue

Donc j’en suis à dire que selon votre position sur terre vous ressentez plus ou moins de clarté, et parfois d’une manière inconnue à vos yeux, dans le sens plus brillant ou plus sombre que vous connaissez d’habitude. Et je viens de démontrer que c’est la hauteur maximale du soleil au dessus de l’horizon qui détermine la clarté. Donc mon problème initial se résume à :

• dans quel intervalle le point de culmination varie dans votre ancien lieu“A” au cours de l’année ?
• dans quel intervalle le point de culmination varie dans votre nouveau lieu“B” au cours de l’année ?

Idéalement on aimerait tracer des graphes de point de culmination pour A et B, et résoudre graphiquement. On pourra, en lisant les abscisses limite, en déduire l’existence de jours dans l’année auxquels le soleil est soit plus haut que le max de ses hauteurs connues au point A, soit plus bas que le min des hauteurs connues au point A.
Ce qui revient à : "la culmination est soit à droite de la borne supérieure de l’intervalle A, soit à gauche de la borne inférieure de l’intervalle A."

Gratuit

A ceux à qui le phrasé mathématique rappelle de mauvais souvenirs, je traduirai en :
Nous allons chercher les jours de l’année pour lesquels le soleil en B est plus haut qu’à la maison en A, ou bien est plus bas qu’à la maison.

Et je vais même le condenser à :

• A quelles dates sortez-vous de l’intervalle bien connu A lorsque vous résidez en B ? (Question 1)
• A quelle date rentrez-vous à nouveau dans cet intervalle familier A ? (Question 2)

Alors comment répondre à ces questions ?

Pour se fixer les idées, soit A une ville de latitude plus haute que B. Basse dans le sens défini précédemment. Le raisonnemment qui suit fonctionne aussi pour l’inverse évidemment.

On va utiliser ma méthode préférée, la méthode graphique. On va tracer les courbes d’angles de culmination sur l’année pour chacun des points A et B, du solstice d’hiver au solstice d’hiver de l’année d’après. Puisque A et B ont des latitudes différentes, les courbes vont en quelque sorte s’empiler comme des assiettes. A étant moins proche de l’équateur que B, la courbe de culmination du soleil en A se trouvera naturellement sous la courbe de B. En d’autres mots, le soleil est plus proche de l’horizon en A, qu’en B.

Je suis maintenant presque prêt à tracer les courbes de culmination pour A et B. On déduit de la loi n°4 que les équations de ces courbes sont du type :

y = f(x) = 90 - x +λ_S

Avec x=la latitude du point considéré, donc λ_A ou λ_B. Hum, j’allais les tracer, quand je m’aperçus qu’il me manquait λ_S…
Uh oh! On a dit en introduction que la latitude du soleil λ_S oscillait entre les deux tropiques, avec un cycle de période 1 an, mais je n’ai pas défini la valeur exacte λ_S(t), c’est à dire sa valeur instantanée à la date t.

Qu’à cela ne tienne, je vais rechercher ici, devant vous, l’expression de λ_S(t), ainsi on pourra injecter cette expression dans la loi n°4, et obtenir y = f(t), au lieu de y=f(x). C’est quand même bien plus sympa de ne plus avoir d’inconnues dans son équation, mais seulement t, une variable bien connu puisqu’elle indique le nombre de jours écoulés depuis le dernier solstice d’hiver.
Pourquoi ? Car c’est au solstice d’hiver que le soleil a son point de culmination minimum au dessus de l’horizon. Le solstice d’hiver est donc un point remarquable, qui va servir d’origine à notre graphique.

Résumé

On va déterminer graphiquement les jours de l’année qui en B qui ne peuvent jamais“matcher” la clarté en A. On le fait graphiquement en dessiner y = f(t) en A, et y = f(t) en B. On ne connait pas f(t), mais on va chercher x(t), puis le réinjecter dans la loi n°4 pour avoir y = f(t).

A ceux qui ne peuvent pas suivre la démonstration ci-dessous car c’est trop technique, rendez vous directement à la loi n°5 et acceptez-là, puis continuez la lecture.

Approximations choisies

Comme toujours dans la nature, les choses ne sont pas des figures parfaites, alors pour simplifier l’étude nous allons faire les approximations suivantes :

1. l’orbite de la terre autour du soleil est considérée comme circulaire.
2. la vitesse orbitale de la terre est considérée comme constante sur l’année, de telle manière que son angle polaire soit proportionnel au quantième du jour.
3. la terre est considérée comme sphérique, de rayon R
4. l’origine des coordonnées polaires de la terre sur son orbite, représentée par θ=0, sera arbitrairement fixée au solstice d’hiver boréal, c’est à dire le 20, 21 ou 22 décembre selon l’année.

Loi n°4

Soit θ l’angle polaire défini dans les rappels en début d’article, alors on a :

θ(t) = (Q(t) - Qdernier solstice hivernal boréal)/365*360

On notera Q₀ = Q_{dernier solstice hivernal boréal}

Q représente le quantième de l’année, c’est à dire le numéro du jour depuis le début de l’année.
Exemple: Q(2 mars 2014) = 60 ; Q₀ = 354
On en déduit θ(2 mars 2014) = (60 - 354) / 365 * 360 = -290° ≡ 70°

Démonstration de la loi n°4

Il s’agit tout simplement d’un corollaire des approximations ci-dessus :
l’angle polaire est proportionnel au quantième du jour, car la vitesse orbitale de la terre est admise comme constante. Le rayon de l’orbite est constant. Donc sa vitesse angulaire est constante et vaut 360° / 365 jours. Donc chaque jour la terre voyage d’un incrément d’angle polaire constant 360/365, ce qui permet de la localiser exactement chaque jour sur son orbite circulaire.

Loi n°5 : λ_S = f(t)

Bien, soit à rechercher la latitude du soleil³ en fonction du jour de l’année. Puisque la loi n°4 nous donne une expression de θ(2 mars 2014) = g(t), t étant le jour de l’année, la loi n°5 va d’abord s’établir comme λ_S = f’(θ), de façon à arriver après à λ_S = f’(θ(t)) = f(t)

Je fais d’abord appel à notre intuition. Quel type de loi attend-t-on ? Une loi linéaire ? Une loi en puissance ? Une loi trigonométrique ?
Euh, à ce stade je n’arrive pas à me décider, car j’ai dû mal à définir ce qu’est ce fameux angle“latitude du soleil”. Donc je reviens à la définition : c’est la latitude d’un point sur terre auquel le soleil est à la verticale à l’instant t, sans se préocupper de sa longitude. Que sait-on sur cet angle ? Il s’annule deux fois par an, aux équinoxes, car le soleil est à ce moment pile à la verticale de l’équateur, lors de son changement d’hémisphère. Egalement, il prend ses valeurs minimale et maximale aux solstices. Les lecteurs observateurs auront remarqué qu’aux équinoxes la durée des jours croît ou décroît le plus vite dans l’année lorsqu’on habite dans des régions tempérées. On peut facilement gagner ou perdre 3, 4 voire 5 minutes de soleil par jour. A l’inverse, autour des solstices, on dirait que la longueur des jours est figée, elle ne varie guère jour après jour. Vous pourrez le vérifier en regardant un calendrier qui montre la durée des jours sur l’année dans votre capitale. Cette fonction est symétrique par rapport à l’équateur : quel que soit le jour considéré dans l’hémisphère nord, il existe une date, à l’opposé dans le calendrier, donc 6 mois plus tard ou plus tôt, à laquelle l’hémisphère sud connaît le même angle, mais inversé de signe. Ceci est dû à la symétrie sphérique de la terre, donc à la symétrie circulaire d’un fuseau considéré à l’instant t. Enfin, puisque l’orbite de la terre est fermée, cette fonction est cyclique, de période 1 an
Bref, une fonction qui s’annule deux fois par an, prend tour à tour un mini et un maxi à 6 mois d’écart, et est symétrique par rapport à l’axe des abscisse…pourrait bien être trigonométrique !

Le cône de révolution

Le cœur du raisonnement est ici. Je vais utiliser un artifice pour mesurer l’angle λ_S. Je vais considérer que, vue depuis le soleil, la terre ne tourne plus, mais par contre son axe tourne autour d’une droite de révolution, faisant avec cet axe un angle ε égal à 23°26’. C’est ce qu’on appelle couramment un changement de repère. Cette droite de révolution est dans le Plan Frontal Solaire (PFS), tel qu’à tout instant, les rayons solaires arrivent perpendiculairement à ce plan. Ainsi, tout point du PFS voit le soleil exactement à la verticale.

Le cône ainsi généré par la révolution de l’axe terrestre autour de cette droite représente l’ensemble des angles de la terre vue depuis le soleil.

Je dis maintenant qu’à tout instant t, l’angle entre l’axe terrestre et le PFS c’est précisément la latitude du soleil. Pourquoi ? Car il faudrait incliner cet axe d’exactement λ_S degrés de cet angle pour que l’équateur touche à nouveau ce plan. Or, vu à l’inverse, il faudrait voyager de ce même nombre de degrés en direction de l’équateur pour à nouveau voir le soleil à la verticale ! J’espère que vous me suivez !

En effet, sur un cercle fuseau de la terre, c’est la même chose de voyager de n degrés le long du fuseau que d’incliner la terre (rotation le long du fuseau) pour retrouver la même situation de verticalité du soleil. C’est là encore juste un changement de référentiel !

Woohoo! Notre problème de définition de la latitude du soleil se résume désormais à :
*quel est l’angle entre l’axe terrestre et le PFS ? Je rappelle que ce plan contient l’axe terrestre aux équinoxes, et qui fait avec la terre +ε ou -ε aux solstices.

L’angle entre une droite et un plan (autrement appelé angle d’incidence), équivaut à l’angle dont il faut incliner ladite droite pour la confondre avec ce plan. Une conséquence est que si je mesure la distance la plus courte du pôle nord au PFS par exemple, alors cette distance définira l’angle de rotation dont il faudrait incliner l’axe terrestre pour“ramener” le pôle nord dans le PFS.

Je vais donc faire un schéma de la situation, et calculer la distance la plus courte entre le pôle nord, représenté par le point P_N et le PFS.

Certains me diront qu’il n’y a pas un unique PFS, mais une infinité de PFS possibles dans la distance terre-soleil, tous parallèles entre eux. Oui, donc ici je ne considère que celui qui coupe la terre en ce centre. Au pire en un point : le centre de la terre, et au plus fort en contenant la totalité de l’axe terrestre, à la date des equinoxes.

Le schéma ci-dessus montre que :

λS(θ) = tan-1(tan ε . cos θ)

Avec θ l’angle polaire du soleil, tel que défini dans les rappels, et ε l’inclinaison sur l’écliptique définie au même endroit.

Eh bien nous voilà avec tous le matériel nécessaire à apporter une réponse à la question initiale. On va remonter petit à petit.

L’équation de la Loi n°5 peut alors s’écrire comme une fonction de t, grâce à la réinjection de la Loi n°4 :

λS = tan-1(tan -ε . cos(Q(t) - Q0)/365*360)

Pourquoi le signe moins devant ε ? Car on choisit arbitrairement un repère qui place le solstice d’hiver à quelques jours seulement de l’origine des abscisses (le 21 ou le 22 décembre correspond donc à la valeur x=-10 ou x=-9). Il est tout à fait imaginable de choisir une origine des abscisses 6 mois plus tard, proche du solstice d’été.

Eh beh j’avais vu juste, il s’agit bien d’une fonction trigonométrique ! On y est presque, on va encore remonter d’un cran plus haut on l’injectant à son tour dans la Loi n°3 :

h(t) = 90° - |λP| + tan-1(tan -ε . cos(Q(t) - Q0)/365*360)

Allez, représentons h(t), avec t variant du 21 décembre au 20 décembre de l’année suivante, pour les villes de Paris (graphe inférieur) et Nice (graphe supérieur).
Les valeurs choisies pour les latitudes sont décrites plus bas, dans la partie "application numérique".
L’échelle choisie est la suivante : 0 à 365 en abscisse, c’est à dire du 1 janvier au 31 décembre, de façon à ce que les abscisses soient directement égales au quantième des jours.
0 à 90° en ordonnée.

Alors comment lire graphiquement les réponses aux questions posées en introduction :
- Je veux connaître la période de l’année où il fait plus clair à Nice qu’il ne fera jamais à Paris.
- Je veux connaître la période de l’année où il fait plus sombre à Paris qu’il ne fera jamais à Nice.

Eh bien pour une fois c’est trivial, il suffit de tracer les horizontales qui passent respectivement par le maxi du graphe de Paris, et les minis du graphe de Nice. Chacune coupera l’autre graphe à des abscisses qui seront les dates recherchées !

Pour ceux pour qui ce n’est pas évident, je formule ceci en d’autres mots : le minimum de hauteur du soleil, donc de clarté, à Paris, est plus bas que le minimum de Nice. Il l’est pour une période prolongée. Tout l’intervalle de l’année dans lequel le graphe de Paris est situé sous le minimum de Nice est précisément cette période où il fait plus clair à Nice qu’à Paris. Le même raisonnement s’applique pour les périodes de plus grande clarté à Nice.

Application numérique

On trouve dans la littérature les valeurs de latitudes suivantes :
λ_Paris = 48.853°N (Notre Dame)
λ_Nice = 43.6969°N (Place Masséna)

Ce qui mène graphiquement, et approximativement aux points d’intersection suivants :

- DPH (Début Périgée Hiver), pour le 316ième jour de l’année, soit le 12 novembre.
- FPH (Fin Périgée Hiver), pour le 33ième jour de l’année, soit le 2 février.

- DAE (Début Apogée Eté), pour le 136ième jour de l’année, soit le 16 mai.
- FAE (Fin Apogée Eté), pour le 216ième jour de l’année, soit le 4 août.

On notera qu’il y a en moyenne 12 jours entre le solstice d’hiver et le 1er janvier (origine du repère des graphes).

Voilà, on a maintenant nos intervalles de lumière inconnue. Exprimées en français, ces réponses deviennent :
à Paris, du 12 novembre au 2 février, il fait sombre comme il ne fera jamais à Nice ;
à Nice, du 16 mai au 4 août, il fait clair comme il ne fera jamais à Paris.

Pour aller plus loin

Pour voir si vous avez bien compris la démarche, je vous soumets un exercice. Vous allez faire le même raisonnement pour la nuit au lieu du jour, afin de connaître les périodes de l’années où il ne fera jamais plus noir qu’il fait la nuit à une autre latitude. Le principe est le même, mais à 180° à l’opposé. En effet, que se passe t-il lorsque le soleil est à son point de culmination à 180° de plus de longitude par rapport à vous ? Fait-il aussi noir que chez vous ? Le point d’anti-culmination vous donnera la réponse. Plus le soleil sera loin sous l’horizon chez vous, et plus une nuit sans lune vous paraîtra obscure. Intéressant, non ?
En prenant le cas particulier des hautes latitudes, qui dépasse les cercle polaires, vous prouverez l’existence du soleil de minuit.

Notes

¹ J’utilise ici le sens qualitatif de proportionnel, et non quantitatif. Je veux dire : la clarté varie dans le même sens que la hauteur du point de culmination. ² J’appelle midi l’heure du jour à laquelle le soleil passe à son point culminant. Ce n’est pas midi sur la montre à l’heure locale. C’est le midi du soleil. Il dépend de la longitude du lieu.

³ Je définis la latitude du soleil comme étant la latitude d’un lieu auquel le soleil passe à son zénith à midi. A cause de l’inclinaison de la terre sur son écliptique, la latitude du soleil ne peut varier que dans l’intervalle [23°26’15" S, 23°26’15" N] dans la notation sexagésimale (base 60), ou [-23.4375, +23.4375] dans la notation décimale.

Références

^R1 En savoir plus sur l’inclinaison de l’axe terrestre sur son écliptique.

^R2 L’inclinaison de l’axe terrestre sur son écliptique est une fonction du temps. Voir l’article Wiki.